Introduction

As we discussed in Lesson 2, in unsteady flow, the energy slope of the stream changes with the stream stage. As a result, the rating curve, the stage discharge relationship, cannot be uniquely determined by the stream stage alone. Before examining the development of more complex rating curves, we review the continuity and momentum equations developed in Lesson 2. We again assume the stream is essentially one dimensional in the direction of flow.

Continuity and Momentum Equations

The conservation of mass equation for an open channel flow system requires that the mass inflow rate less the mass outflow rate equal the change in mass storage. The equation can be express as

u  ∂A ∂y  ∂y ∂x +u  ∂A ∂x +A  ∂u ∂x +  ∂A ∂y  ∂y ∂t =q

2.7

where u(x,t) is the mean x-velocity at time t, y is the water depth in the reach, A is the cross sectional area, and q is the flow rate.

For a rectangular channel with width b, the equation simplifies to

y  ∂u ∂x +u  ∂y ∂x +  ∂y ∂t =  q b

2.8

The momentum balance equation is a restatement of Newton's second law. The sum of the forces acting on the system equals the time rate of change of the momentum, the product of the fluid mass and velocity. The momentum balance for the stream can be described by the equation

∂u ∂t +u  ∂u ∂x +  uq A +  g A y  ∂y ∂x =g(S0-Sf)

2.17

where S₀ and S_f are the channel slope and friction slope, respectively, and g is the gravitational constant.

The continuity and momentum equations are a coupled system of nonlinear, first order partial differential equations. The numerical methods that are commonly used for the approximate solution of the equations are basically of four different types:

1. Finite difference methods that solve the underlying characteristic equations in a curvilinear coordinate system
2. Explicit finite difference equations for a rectangular x-t coordinate system
3. Explicit finite difference methods for the original equations on a rectangular grid system, and
4. Implicit finite difference methods for the original equations, also on a rectangular grid.

Several of these methods will be explored in Lessons 9.

Classification of Equations

Various levels of complexity of the continuity and momentum equations can be developed by assuming that the discharge, Q, is related to the friction slope, S_f via the equation,

Q=CmαSf1/2

8.1

where C and α are parameters, m = A/P, and P is the wetted parameter.

The discharge equation, Equation 8.1, can be expressed as

Q=Qs [ 1-  1 S0  ∂y ∂x -  V S0g  ∂V ∂x -  1 S0g  ∂v ∂t ] 1/2

8.2

where Q_s is steady, uniform flow discharge. The equation is known as a looped rating curve (Figure 8.1). The two points in Figure 8.1 represent the maximum flow (A) and maximum depth (B). The loop's width depends on the magnitude of the secondary terms in Equation 8.2.

Figure 8.1. Looped rating curve.

In the kinematic wave approximation, the momentum model is simply Q=Q₀. The flow regime is uniform and unsteady. The water surfaces and the streambed are parallel to one another and to the energy grade line. Alternatively, the discharge is a single value function of depth.

Combining the flow and (kinematic) momentum equations yields

1 c  ∂Q ∂t +  ∂Q ∂x =0

8.3

where c is the kinematic wave speed, computed as

c=  dQ dA =  1 T  dQ dy

8.4

In the kinematic model, both the inertia and pressure terms are small in comparison with the friction and gravity terms. There is therefore no attenuation of the kinematic wave; it changes shape at the kinematic wave speed.

The diffusion analogy solution is based on the relation,

Q=Qs [ 1-  1 S0  ∂y ∂x ] 1/2

8.5

The continuity and the above momentum equation can be combined to yield

∂Q ∂t +c  ∂Q ∂x =D  ∂2 Q ∂x2

8.6

where c = 1/T(dQ/dy) is a coefficient that dictates the translational characteristics of the flood wave while D,a diffusion coefficient, represents the attenuation of the flood wave. The diffusion model effectively neglects the inertial terms in the momentum equations; that is the inertial term is small relative to the pressure, friction, and gravity terms.

The representation of Q given in Equation 8.2 is referred to as the complete dynamic wave solution; the streamlines and water surface profiles are not parallel.

As shown by Henderson (1966), friction typically governs the momentum of the flow; the effect of the slope of the water surface on the flow momentum is relatively small. Furthermore, the impacts of acceleration and convection on the momentum flow component are small relative to friction, e.g. 1:1000. The continuity and momentum equations can then be expressed (Raudkivi, 1979),

∂A ∂t +  ∂Q ∂x

8.7

∂y ∂x +  Q2n2 A2m4/3 =S0

8.8

where lateral inflow has been neglected.

The discharge equation coupled with the conservation equations can represent a range of open channel flow conditions. The models include the

1. kinematic wave approximation,
2. the diffusion analogy approximation, and
3. the complete dynamic wave model.

In the kinematic wave model, the flow regime is uniform and unsteady. In the diffusion model, the inertial terms of the momentum equation are ignored. In contrast, in the dynamic wave model the streamlines and water surface profile are no longer parallel.

Overview of Complex Stage Discharge Models

As we have seen in previous lessons, the stage at a gaging station for a given discharge, assuming subcritical flow conditions, is influenced by downstream control elements. Moreover, the control may act independently for some range of stage, or it may act in association with other controls. For a given discharge, the effect of the control elements on the stage at a gaging station is referred to as backwater. If the control elements are unchanging, the backwater for a given station is also unvarying; the discharge is then a function of stage only. In addition, the slope of the water surface at the stage is invariant. If however, the control elements are variable for a given discharge, the stage and slope are also changing. Discharge in this case is related to both stage and water surface slope. Since the slope between two points is simply the fall between the two points, hydrologists typically express discharge as a function of discharge and fall.

Stage fall discharge models are determined empirically from observational data of (1) discharge, (2) stage at the base gage (usually upstream), and (3) the fall of the water surface between the base gage and the auxiliary gage. The rating curve methodology involves:

1. Determining a base relationship between stage and discharge for uniform flow or for a fixed backwater conditions. The discharge is Q_r.
2. The relation between stages and fall for uniform flow or fixed backwater are then developed. The falls are referred to as rating falls, F_r. Figure 8.2 illustrates the general relationships.
3. The ratios of the discharges under variable backwater conditions, Q_m, to Q_r are correlated with the ratios of the measured falls, F_m to F_r, or
   
   Q_m/Q_r=f(F_m/F_r)          8.9

Figure 8.2. Relationship between stage and fall for uniform flow.

The functional form, f, of the model is dependent on the channel features that control the rating curve. A commonly used model is

Q_m/Q_r=f(F_m/F_r)^N         8.10

where 0.4 < N < 0.6.

The fall between a base and auxiliary gage may not always provide a true representation of the water surface slope between the sites. The water surface affected by backwater is usually not a plane surface between the points in a reach; sinuosity of the channel produces variations in the height of the water surface. The water surface will also exhibit curvature resulting from variations in the channel's cross section. Slope determined from differences in stage is a chord connecting the water surface elevations. It may not represent the slope of the water surface at either end of the reach.

The problem is compounded since no channel reach is completely uniform. The cross sectional area varies considerably from point to point in the stream channel. Shoals, riffles, rapid, or bends affect the water surface slope and the energy gradient.

The location of the gages at the ends of the reach can also impact the recorded gage heights and the slope. For example, if a gage in located on the inside or a sharp bend and the other gage on the outside of a similar bend, the slope computed from the stage record can be dramatically different from the average water surface slope.

Finally, it may not be possible to set the gages to the same datum. The difference in datum can be a large percentage of the total fall if the fall is small. The computed slope, as determined from the gages, would not indicate the true water surface slope since it includes the difference in the datum.

The ramifications of these practical considerations is that theoretical models between stage, fall, and discharge cannot be directly applied. The models are usually determined empirically by discharge measurements made over a wide range of backwater conditions. Stage fall discharge ratings are of two general types:

1. rating fall constant—these relationships are developed for uniform channels; the water surface profile between gaging stations does not exhibit appreciable curvature.
2. rating fall, stage dependent—these relationships are developed if
   1. there is significant curvature of the water surface,
   2. the reach is nonuniform,
   3. a submerged section control exists in the reach but the control does not become completed submerged even at high discharges, or
   4. a combination of these factors.

There are two general principles that "govern" backwater effect. The first principle is that for a given stage at the variable control element, backwater decreases at the base gage as the discharge increases. Secondly, backwater decreases at the base gage as stage decreases at the variable control element; this presumes a constant discharge.

The following sections discuss the development of the stage fall discharge rating curves.

Rating Fall Constant

The water surface profile is parallel to the stream bed in uniform stream channels. The rating fall, F_r in uniform flow (no variable backwater) is the same at any stage. The stage discharge relationship can then be described by the Chezy equation,

Q=CA(RS)^0.5         8.11

where C is the Chezy coefficient that represents the frictional losses occurring as water flows over the bottom and sides of the stream channel. It is related to the Darcy friction factor, f, that is used in pipe flow, or

C=(8g/f)^0.5         8.12

where g is the gravitational coefficient. R is the hydraulic radius, e.g. the cross sectional area divided by the wetted perimeter, P, and S is the energy slope. In uniform flow, S is the slope of the channel bed. The energy slope can also be represented as S=F_r/L, where r denotes the base rating condition.

If a downstream tributary imposes variable backwater on the stream reach, the measured fall, F_m, and discharge, Q_m is less at a given stage than the given by the uniform discharge equation. Assuming the measured slope or fall represents the slope at the base gage, the stage discharge curves define a family of curves that are constant except for differing values of fall. The relationship can be summarized as

Q/Q_r=(F/F_r)^0.5         8.13

The variable backwater discharge can then be expressed from Equation 8.13,

Q=Q_r(F/F_r)^0.5         8.14

In situations where the base rating is controlled by a downstream dam, a constant rating fall can also occur. The water surface profile will again be approximately parallel to the channel bed at all discharges provide the curvature in the backwater profile is not significant. Typically F_r is assumed to be equal to 1 foot. In this special case, Equation 8.14 reduces to

Q=Q_rF^0.5         8.15

Equation 8.15 is known as the unit fall method.

Although a constant rating fall is not usually encountered in natural streams, if discharge measurements cover the entire range of streamflow, there is no need to use more complicated equations. The measurements however have to conform to a constant rating fall. Theoretically this occurs when the curvature of the profile and the velocity head changes are truly negligible.

Non Constant Fall Methods

Overview of Rating Fall and Stage

In streams where backwater is a factor in the rating curve, fall is typically a function of the stage. The relationship may be linear or nonlinear.

An example of a linear relation between stage and fall is illustrated in Figure 8.3. A gaging site is located at the Dalles, Oregon on the Columbia river. The stage discharge relation at the gaging site is affected by reservoir releases at Bonneville Dam, a distance of more than 80 miles downstream. The auxiliary gage is located at Hood River bridge 19 miles downstream from the base gage. Fall is linearly related to the stage.

Figure 8.3. Linear relationship between stage and fall on Columbia River, The Dalles, OR.

A complex stage fall relationship is shown in Figure 8.4. The data are for the Ohio River, Metropolis, Illinois. At the auxiliary gage, the stage discharge curve is affected only at the lower stages by a constriction; the backwater from the constriction causes fall to decrease with stage in the lower sections of the reach. At higher stages, the constriction has minor impact; fall increases with stage.

Figure 8.4. Nonlinear relationship between stage and fall on Ohio River, Metropolis, IL.

It situations where a section control is located downstream from a base gage, it is important to identify when the backwater effect is absent at the base gage. No backwater effect occurs when the tailwater at the section control is below the crest of the control. Since most artificial controls are broad crested, submergence is effective only when the tailwater rises to a height above the crest that is equal to or greater than 0.7 times the head on the control. As a result, a straight line of initial submergence may be drawn on the stage fall curve; the line passes through the coordinates representing the elevation of the control crest and zero fall that has a slope of 3 (feet of stage per 1 foot of fall).

In reality, the exact position and slope of the line is dependent on the placement of the downstream auxiliary gage. If the auxiliary gage is just downstream of the section control, the line of initial submergence is as discussed in the preceding paragraph. If not, the submergence line will intersect the elevation of the crest at a value of fall greater than zero; the slope of the line will depend on the hydraulic features of the station. Field data are necessary to identify the graphical coordinates of the line of initial submergence. Free fall discharge occurs for all data points lying below the line of initial submergence; those above are affected by variable backwater. Moreover, if the tailwater gage is close to the control, the fall ratio curve should closely fit the theoretical model,

Q_m/Q_r=(F_m/F_r)^0.5         8.16

A rating gage that has no section control is analyzed as in the previous section. The principal difference between the rating fall constant method and this approach is that the rating fall for any stage is obtained from the rating fall curve. For a gaging station with a base gage that has a section control, the rating proceeds in two steps. First the free part of the rating is analyzed (no backwater effects). Secondly, the variable backwater effect is analyzed assuming there is no section control.

Discharge Determination

Three graphical relationships are necessary to determine the discharge. They include:

1. the relationship between stage and rating fall, F_r
2. stage versus rating discharge, Q_r
3. Q_m/Q_r versus F_m/F_r

The computation of discharge, Q_m, for a given stage and a given fall, F_m consists of the following steps:

1. determine the fall rating, F_r, for the known stage
2. compute the ratio F_m/F_r
3. using tabular representation of the data, determine the ratio, Q_m/Q_r
4. from the stage discharge information, determine the rating discharge, Q_r, for the known stage
5. determine Q_m=(Q_m/Q_r)Q_r

Variable Slope and Changing Discharge

In situations where channel control is effective, the effect of changing discharge on a rating curve produces a loop curve. An example is shown in Figure 8.5. In a loop curve, the discharge for a given stage is greater when the stream is rising than when it is falling. In a simple stage discharge relation for steady flow, data obtained on the rising stage are located to the right of the curve; measurements for a falling stage plot to the left of the rating curve. The variation for the steady flow rating curve is significant only when the slope of the stream is relatively flat and the rate of change of discharge rapid. At gaging sites where this occurs, the discharge rating must be developed by adjustment factors that relate steady to unsteady flow.

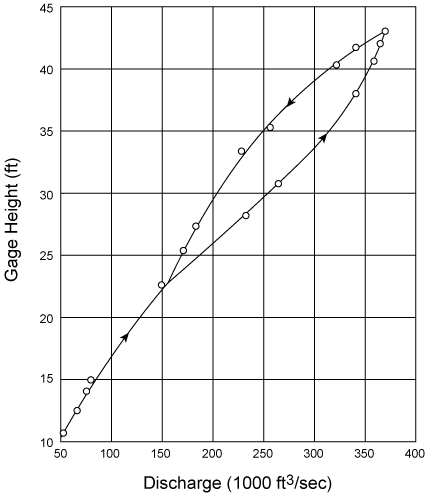Figure 8.5. Variable slope and discharge resulting in looped rating curve.

A relation between flow discharge under steady and unsteady conditions at the same stage can be expressed [see Equation 8.2],

Q_m/Q_c=[1+1/(S_cu_w)(dh/dt)]^0.5         8.17

where Q_m is the unsteady flow discharge, Q_c and S_c are the discharge and energy slope for steady flow at the same stage, u_w is the wave velocity (celerity), and dh/dt is the rate of change of the stage with respect to time, t. The time derivative is considered positive with increasing stage.

The wave velocity, u_w can be expressed as

u_w=(1/B)(dQ/dh)         8.18

where B is the channel width at the water surface and dQ/dh is the slope of the stage discharge curve for constant flow conditions. Table 8.1 summarizes the variation in the wave velocity to the mean velocity, V_m for various channel types based on using the Manning and Chezy equation for computing the mean velocity. The most probable value in natural channels is 1.3.

Table 8.1. Variation in wave velocity to the mean velocity for various channel types.
Channel Type	Ratio (uw/Vm)
	Manning Eqn.	Chezy Eqn.
Triangular	1.33	1.25
Wide rectangular	1.67	1.50
Wide parabolic	1.44	1.33

Equation 8.17 can be used to explain the significance of changing discharge in flat streams during rapid changes in discharge. Only for these conditions will the right hand side of the equation differ significantly from unity. The absolute values of dh/dt are large during rapid changes in discharge. In flat streams, the energy slope and celerity are small. The combination of a large change in stage and small values of the energy slope and celerity increases the right hand side of the equation to a number greater than 1.0; similarly, it is significantly smaller than 1.0 during a falling stage, dh/dt < 0.

Rating Adjustment for Changing Discharge

There are two principal methods to adjust the discharge for changing slope. Both methods are based on Equation 8.17. In the Boyer method, a solution of Equation 8.17 is generated with individual measurements of u_w and S_c. Numerous discharge measurements are made for both rising and falling stage. Measured discharge, Q_m, is plotted against stage and along side each plotted point, the value of dh/dt is noted. A trial rating curve, representing steady flow conditions where dh/dt=0, is fit to the discharge measurements. The values of Q_c from the curve corresponding to the stage of each discharge measurement are used in Equation 8.17 and the observed change in stage is used to compute the adjustment factor, 1/(S_cu_w). The computed values of q/(S_cu_w) are plotted against the stage and a smooth curve drawn through the points. If the plotted values of the adjustment factor are widely scattered about the curve, the Q_c is modified to produce new values of 1/(S_cu_w). Figure 8.6 depicts the process.

The adjustment of subsequent discharge measurements for plotting on the Q_c rating curve begins by entering the adjustment factor curve with the stage measurement and obtaining 1/(S_cu_w). The observed value of dh/dt is used with the factor to compute (1+S_cu_wdh/dt )^0.5. The term is then divided into the measured discharge, Q_m to determine Q_c.

Figure 8.6. Adjusting rating curve for changing discharge using the Boyer method.

If discharge is required from the Q_c rating curve during a period when the stage and rate of change in stage are known, the procedure in the preceding paragraph is again used to determine (1+S_cu_wdh/dt)^0.5. This term is then multiplied by Q_c which is obtained by entering the Q_c rating curve with the known stage. The product is the required discharge, Q_m.

The second approach is the Wiggins method. It is a convenient methodology for adjusting measured discharge, Q_m for the effect of changing discharge. The converse procedure of computing discharge for unsteady flow, Q_m from steady flow is complicated. As a result, Wiggins method is used only for those stations where occasional adjustment of measured discharge at high stages is necessary. If the discharge is affected by changing stage on numerous occasions, the Boyer method should be used. The Wiggins method does not require numerous discharge measurements.

In the Wiggins method, the discharge measurement are used to define the steady flow rating; the rating is used directly with the gage height record to obtain daily value of discharge. The procedure is justifiable in streams where the discharge is affected by changing discharge on only a few days each year. It is generally found that the discharge adjustment is less than 10 percent. On the affected days, the discharge from the steady flow rating curve will be underestimated by a small percent when the discharge is rising rapidly; it is overestimated when the discharge is falling rapidly. The discrepancies are compensating and usually the streamflow record is not significantly impacted.

The Wiggins method is simplified by several figures which are used to determine the energy slope, S_m at the time of discharge measurement, Q_m for differing combinations of mean velocity, u_m, and hydraulic radius, R. The figures represent different values of Manning's roughness coefficient ranging from smooth bed and banks to very rough streambed conditions. The procedure involves first determining the increment of energy slope, (1/u)dh/dt attributable to changing discharge for combinations of u_m and dh/dt. It is assumed that u_w = 1.3u_m. Next a factor is determined to apply to the measured discharge, Q_m to yield the steady flow discharge, Q_c. The factor can be expressed as

[ Sm-  1 uw  dh dt Sm ] 0.5

8.19

where S_m is the base slope. The factor is given for differing combinations of S_m and of (1/u_w)(dh/dt). The factor depends on whether the stage is rising or falling. Both the measured, Q_m, and the adjusted, Q_c, discharge are entered in the list of discharge measurements and are plotted on the rating curve.

Variable Backwater and Changing Discharge

If the rating curve for a gaging site is affected by both variable backwater and changing discharge, the rating should first be analyzed by variable backwater using the fall ratings method. The fall rating method is the only method versatile enough to incorporate these two factors.

Changes in Discharge Rating with Slope

As we have discussed previously changes in the channel geometry resulting from scour and fill, flow conditions altered from vegetal growth will impact the rating curve where slope is a factor. If field data, discharge measurements, demonstrate a shift in the rating curve, shift should be applied to the Q_r rating curve for the backwater effects, or to the Q_c curve to reflect changing discharge.

Rating Curves and Computer Models

The previous techniques have relied almost exclusively on empiricism, a series of graphical relationships. In contrast, mathematical simulation models of open channel flow can be used for the prediction of stream discharge for a range of hydrologic events. In conjunction with observational data, the parameters of the model could be estimated using conventional parameter identification techniques.

A simplified example of the approach can be illustrated by considering Manning's equation. It is assumed that the acceleration head is negligible. Discharge measurements are made for the sole purpose of determining Manning's roughness coefficient, n. The estimate of n is not the true value of the parameter; it incorporates all the possible error sources in the flow equation, including the energy slope variation in the reach. Typically, the computed value of n would vary with stage.

Manning's equation can be expressed as

Q=KS^0.5         8.20

where Q is the discharge, S is the energy gradient, and K is the conveyance,

K=δ/nAR^2/3         8.21

where A is the cross sectional area and R is the hydraulic radius. Equation 8.21 can be expanded to a reach as

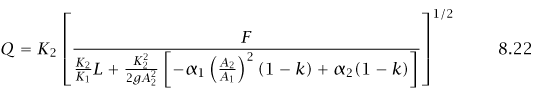
where the subscripts 1 and 2 denote the upstream and downstream cross sections respectively. F is the fall in the reach, L is the reach's length, g is the acceleration constant, αis the velocity head coefficient; its value is a function of the reach's velocity distribution. k is an energy loss coefficient; it is zero for contracting reaches and 0.5 for expanding reaches.

Data for the reach would define the relation between the stage and K, A, and α. Given the stage data, Equation 8.22 is solved to compute Q.

Discharge Rating using Velocity

In many gaging sites it is not possible or feasible to use a slope parameter for stations for which there is no simple stage discharge relationship. The slope may be so flat as to prohibit an accurate assessment of the fall occurring in a reach. Also, the acceleration head can be significant as on tidal streams or in streams with hydropower generation. In these cases, a velocity index is used to develop the stage discharge relation.

The underlying principle in stage velocity discharge models is based on a continuous stage record. The data provide a mean of obtaining a continuous record of cross sectional area from a relation of area to stage. Provided a continuously recorded velocity index can be related to the stage and mean velocity in the cross section, the product of the area and the velocity yields the discharge at any time. The development of the recorded index velocity to the stage and the mean velocity requires discharge measurements. The discharge data also provide the necessary cross sectional areas for the stage area equations.

The velocity index is determined using four types of instrumentation:

1. standard current meter
2. deflection meter
3. acoustic velocity meter
4. electromagnetic velocity meter

The most basic approach for recording velocity at a fixed point in a cross section involve both the standard current meter and the deflection meter. They are limited to streams where damage by both boats and debris is minimal. The acoustic velocity meter integrates the transverse velocity and historically has been used in larger rivers. The electromagnetic velocity meter is used in smaller streams; it is used to obtain a continuous record of point velocity.

Discharge Rating using Velocity—Standard Current Meter Method

The simplest application of the velocity index method involves the use of a standard current meter. The unattended current meter is typically anchored in a fixed position at a depth below the minimum expected stage. It should be located in the central core of the flow isolated from the influence of the stream banks; the streamlines are parallel and at right angles to the measurement cross section.

Discharge measurements are used to calibrate the stage velocity discharge relationship. The cross sectional areas shown by the discharge measurements are used with the stream stage to determine the stage area relation; the equation can be extrapolated by field data. The mean velocities shown by the discharge data are used graphically relating the mean velocity to the stage, and to the index velocities available from the current meter. Extrapolation of the data would be facilitated if (1) a vertical velocity curve is available at the site of the current meter and (2) the mean velocity in the vertical is related to the mean velocity in the measurement cross section.

These ideas can be illustrated by assuming that the vertical velocity curve at the measurement (index) site can be expressed as

u_i=1.16u_m(y/D)^0.16         8.23

where u_m is the mean velocity in the vertical, D is the water depth, and u_i is the velocity at height y above the streambed. Figure 8.7 depicts this relationship for several different gage heights. Figure 8.7 is based on the assumption that the ratio of the mean velocity in the measurement cross section is equal to 0.92. The mean velocity from Figure 8.7 is multiplied by the appropriate cross sectional area to determine the discharge.

Figure 8.7. Discharge rating using current meter velocity measurements.

Although the approach is conceptually straight forward, the current meter methodology has several disadvantages. The meter is susceptible to damage; there is also the tendency for the meter to become fouled after long period of immersion. Constant servicing is usually required and sediment affect unattended current meter operation.

Discharge Rating using Velocity—Deflection Meter Method

Deflection meters provide a velocity index in small canals and streams where there is no simple stage discharge relationship. This is typically caused by tidal effects or from downstream gate operations that regulate the flow regime.

Deflection meters have a submerged vane that is deflected by the force of the current. The deflection is roughly proportional to the velocity of the current impinging on the vane. It is transmitted mechanically or electrically to a recorder. The mean velocity of the stream is determined from discharge measurements; the mean velocity can then be related to the deflection and stage. The meter ideally should be located in midchannel in a straight reach.

There are two types of deflection meters: the vertical axis and horizontal axe deflection vanes (see Figures 8.8 and 8.9) In a vertical axis deflection meter, the force of the current turns the vertical shaft; this motion is transmitted to a graphical or digital recorder. The most serious limitation of the meter is that its tendency to collect floating debris which affects the calibration of the vane. Also, there is a high degree of bearing friction that causes insensitivity at low velocities.

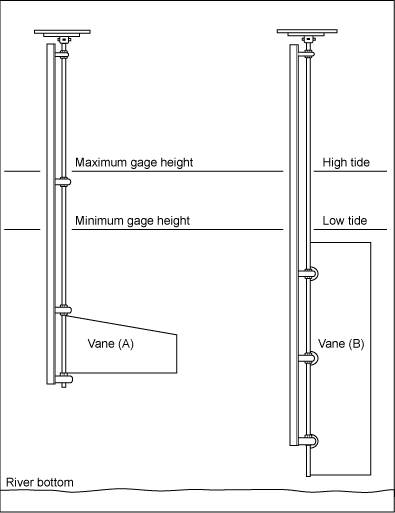Figure 8.9. Vertical axis deflection meter.

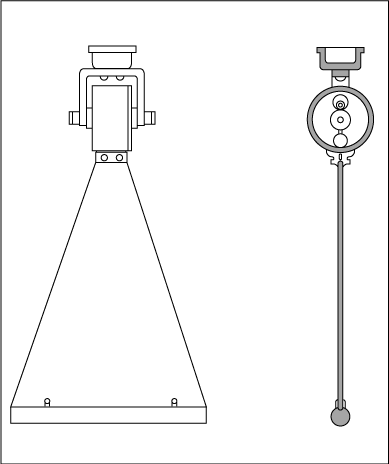Figure 8.9 Pendulum type horizontal axis deflection meter.

The horizontal axis deflection meter was designed to overcome the limitations of the vertical axis deflection meter. The vane can be installed totally submerged eliminating the debris issue; there is little danger of ice damage as well. Its light weight also improves its low velocity characteristics. The force on the horizontal vane again causes it deflect which is directly related to the flow velocity.

Example rating curves are shown in Figure 8.10. The rating curves were derived from discharge measurements. The deflection units are indicative of the velocity in a single vertical in the channel. The velocity curve depicts the relation between the deflection units and the mean channel velocity; in this case, stage is not a factor. The stage at the discharge measurements was used to construct the area curve (which relates stage to cross sectional area). Discharge is determined by multiplying the area by the mean velocity.

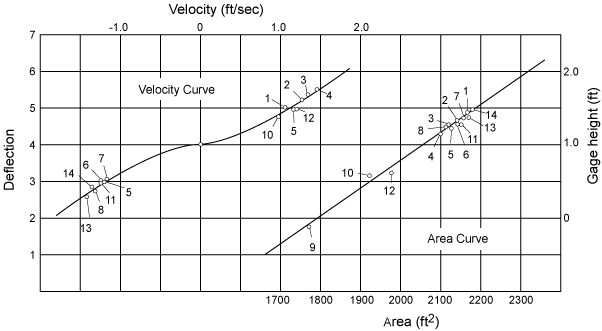Figure 8.10. Rating curve derived from deflection meter data.

Discharge Rating using Velocity—Acoustic Velocity Meter

The principal advantage of acoustic velocity meters is that they provide a continuous record of the discharge of large rivers where the acceleration head cannot be ignored. Acoustic velocity meters are based on the principle that the velocity of sound prorogation through a fluid in motion is the sum of the fluid velocity and the acoustic propagation rate through the fluid. Acoustic pulses that are transmitted in the flow direction will traverse a given path in a shorter time that those transmitted in the opposite direction. The transit time difference is a measure of the average value of the water velocity at the elevation of the acoustic path, the line velocity. The line velocity does vary with stage since the transducers that transmit and receive the acoustic pulses are installed at different fix elevations. The stage recorder provides baseline stage data and an index of the cross sectional area.

The propagation of the acoustic signal is affected by (1) temperature gradients, (2) proximity of the stream boundary, (3) air entrainment, (4) sediment load, and (5) aquatic vegetation. The development of even extremely small temperature gradients in the water column have the potential for causing refraction of the acoustic signal. In streams with poor mixing, the variation in solar radiation and air temperature can cause these gradient to develop. The problem can be minimized, though not eliminated, by locating the acoustic path near mid depth of the stream channel.

A portion of the acoustic signal will be reflected from the air water interface and/or streambed. The reflected components arrive at the receiving transducers almost simultaneously but out of phase with the primary pulse. This phenomenon is dependent upon the ratio of the path length to a distance to a boundary and the frequency of the transmitted signal. Data suggest that broad, shallow channels are questionable sites.

The acoustic signals can be attenuated by air bubbles that are entrained in the water. The bubbles absorb and reflect the acoustic signal; the phenomenon is similar to fog as it absorbs and reflects light. The general recommendation is to locate these systems far away from spillways or other sources of entrainment.

The sediment load of a stream or river can also be expected to affect the acoustic signal. The reflection and scattering of acoustic signals results in attenuation that is influenced by the sediment load concentration, the size of the sediment particles, water temperature, and the length of the acoustic path.

Aquatic vegetation has a variable impact on the acoustic signal. The effects are dependent upon the location and density of weed growth. Dense growth may actually block the signal completely.

All of these factors should be considered in the selection of an acoustic velocity site. The most important consideration is to ensure, whenever possible, reliable acoustic transmission and reception. This usually requires the acoustic path to be as short as possible to minimize the acoustic refraction and attenuation losses.

The discharge calculations are preceded by calibrating the acoustic velocity system. Discharge measurements are first made to obtain measured values of the cross sectional area, A, and the mean velocity in the cross section at right angles to the streamlines, u_m. The measured values of A are correlated with stage to produce a graphical stage area curve. The digital processor the acoustic velocity system produces a velocity index, I. Measured values of u_m are divided by the concurrent value of I to obtain the parameter K, the ratio between the mean stream velocity and the velocity index. K includes proportionality coefficients and aa, the acute angle between the streamline of flow and the acoustic path. These K values are then correlated with stage; an example is shown in Figure 8.12.

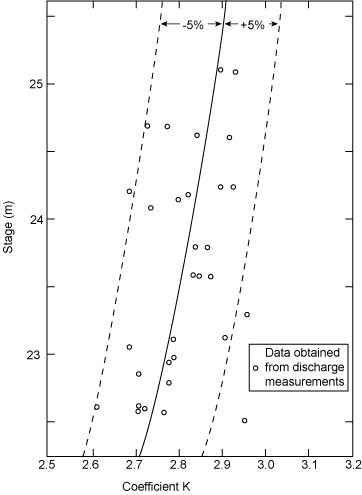Figure 8.11. Discharge coefficient K values correlated with stage.

The discharge for any given value of I is determined by first reading the concurrent value of stage. The stage is then used to determine the value of K, via Figure 8.12 and the cross sectional area, A. The discharge is then given as Q=KIA.

Alternatively in lieu of graphical relationships, equations can be used relating A to stage and K to stage. Two assumptions have to satisfied however. First, the relation between the area and the stage, H, is stable and described by the equation,

A=C₁+C₂H+C₃H²         8.24

where C_i are parameters. Secondly, the parameter Kcan be expressed

K=C₄+C₅+C₆H²         8.25

where again C_i are parameters.

Provided sufficient discharge measurements are available, the parameters can be estimated using conventional least squares. If this is not possible, the parameters are obtained from the graphical relations of A versus H and K versus H. Coordinates of three significant points are selected on one of the graphical relation and then substituting these values in the appropriate equation. The equations are then solved simultaneously to produce the required parameter values. The process is then repeated for the K relation. The six parameter values, C_i, are then used to determine the discharge,

Q=(C₄+C₅+C₆H²)(C₁+C₂H+C₃H²)I         8.26

Discharge Rating using Velocity—Electromagnetic Velocity Meter Method

The electromagnetic velocity meter is based on the principle that a voltage is induced in an electrical conductor moving through a magnetic field. The magnitude of the induced voltage is proportional to the velocity of the conductor for a given field strength. The conductor in a electromagnetic velocity meter is the flowing water.

The observed point velocities from the electromagnetic velocity meter are used as indices of the mean stream velocity. The methodologies are the same as discussed previously when the standard current meter and the deflection meter were the instruments used to measure point velocities.

The commercially available electromagnetic velocity meters are of two general types. One type of meter consists of a nonmagnetic tub through which the water flows, two magnetic coils, electrodes in the walls of the tube between the magnetic coils, and circuity to transform the induced voltage into a metered velocity. The second consists of probe containing an electromagnet internally and two pairs of external electrodes in contact with the flowing water. Flow around the probe intersects with the magnetic flux lines causing voltage changes. Again electrical circuits transform these fluctuations into velocities.

In either type of meter, higher velocities are more accurately measured than low velocities. The same procedures apply to the unattended operation of the meter. It is securely anchored in a fixed position below the minimum expected stage. Usually, a recording stage gage is operation in association with the velocity meter.

The analysis of the data from the velocity meter proceeds identically as with the fixed standard current meter. The mean velocity for the measurement cross section is again obtained from discharge measurements; the data are correlated with concurrent stage and point velocity. Cross sectional area is then related to stage, and the product of the area and the mean velocity yields the discharge.

Lesson 8 Summary

In many streams, unsteady flow predominates, and the energy slope of the stream changes with the stream stage. As a result, the rating curve, the stage discharge relationship, cannot be uniquely determined by the stream stage alone. This lesson examined a number of commonly used methodologies to develop rating curves for stream with unsteady flow regimes.

The following terms and concepts were introduced in this lesson and should be mastered prior to continuing with on to Lesson 9. Selecting a link in the list below will result in a jump to the portion of the lesson material above that covered the relevant material so that it can be reviewed as necessary.

• Definitions
  • backwater
  • stage fall
• Concepts
  • open channel flow continuity and momentum equations
  • numerical solution techniques for solving continuity and momentum equations
  • kinematic wave discharge equation model
  • diffusion equation discharge model
  • complete dynamic wave equation discharge model
  • looped rating curve
  • rating fall constant method
  • unit fall method
  • non-constant fall methods
  • Boyer method
  • Wiggins method
  • discharge rating using standard current meter method for velocity
  • discharge rating using deflection meter method for velocity
  • discharge rating using acoustic meter method for velocity
  • discharge rating using electromagnetic velocity meter

Lesson 9 Preview

The discharge in many coastal streams experience tidal influence during some portions of the year. Developing rating curves for these streams is important since they are frequently the streams that experience seasonal flooding and resulting property damage. Lesson 9 will address the empirical development of stage discharge models for tidally influenced stream and a simplified numerical model of the unsteady flow equations.